Definition: A signal is a function representing a physical quantity or variable, typically containing information about the behavior or nature of a phenomenon. There are various types of signals classified based on the nature of the information they contain.
For example, in an RC circuit, the signal may represent the voltage across the capacitor or the current flowing in the resistor.
Representation of Signal: Mathematically, a signal is represented as a function of an independent variable t, where t usually represents time. Therefore, a signal is denoted by x(t).
Also read: What is a Signal?
Classification of Signals
Signals are classified into different types, and the representation and processing of a signal depend on its type.
The different types of signals are as below.
- Continuous Time and Discrete Time Signals
- Analog and Digital Signals
- Real and Complex Signals
- Deterministic and Random Signals
- Even and Odd Signals
- Periodic and Not Periodic Signals
- Energy and Power Signals
- Causal and Not Causal Signals
1. Continuous Time Signals and Discrete Time Signals
A continuous-time signal, denoted as x(t), has a continuous variable t. If t is a discrete variable, meaning x(t) is defined at discrete times, then it’s termed as a discrete-time signal. Since a discrete-time signal is defined at discrete times, it’s often represented as a sequence of numbers, denoted by {xn} or x[n], where n is an integer.
- Continuous-time signals → x(t), vary continuously over time.
- Discrete-time signals → x[n], are defined at specific discrete times and represented as sequences of numbers.
A discrete-time signal x[n] might represent a phenomenon where the independent variable is inherently discrete. For example, the daily closing stock market average inherently evolves at discrete points in time, namely at the close of each day.
Sampling
A discrete-time signal x[n] can be obtained by sampling a continuous-time signal x(t), such as…
x(t0),x(t1), …,x(tn),…
or in a shorter form as
x[0],x[1], …,x[n], …
or x0,x1,…,xn,…
where we understand that
xn = x[n] = x(tn)
and xn‘s are called samples and the time interval between them is called the sampling interval.
When the sampling intervals are equal (uniform sampling), then
xn = x[n] = x(nTs)
where the constant Ts is the sampling interval
2. Analog and Digital Signals
If a continuous-time signal x(t) can assume any value in the continuous interval (a, b), where a may be -∞ and b may be +∞, then the continuous-time signal x(t) is termed an analog signal.
On the other hand, if a discrete-time signal x[n] can only take on a finite number of distinct values, then we refer to this signal as a digital signal.
3. Real and Complex Signals
A signal x(t) is classified as a real signal if its value is a real number, and it is categorized as a complex signal if its value is a complex number.
A general complex signal x(t) can be represented as a function of the form:
x(t) = x1(t) + jx2(t)
where x1(t) and x2(t) are real signals and j = √-1
4. Even and Odd Signals
Even Signals: A signal x(t) or x[n] is referred to as an even signal if
x(-t) = x(t)
x[ -n] = x[n]
Examples of even signals are given in the image below.
Odd Signals: A signal x(t) or x[n] is referred to as an odd signal if
x(-t) = -x(t)
x[-n] = -x[n]
Examples of odd signals are given in the image below.
Any signal x(t) or x[n] can be represented as the sum of two signals, one of which is even and the other odd. That is,
x(t) = xe(t) + xo(t)
x[n] = xe[n] + xo[n]
Where,
- The even part of x(t) is calculated as: xe(t) = 1/2 * {x(t) + x(-t)}
- The odd part of x(t) is calculated as: xo(t) = 1/2 * {x(t) – x(-t)}
- The even part of x[n] is calculated as: xe[n] = 1/2 * {x[n] + x[-n]}
- The odd part of x[n] is calculated as: xo[n] = 1/2 * {x[n] – x[-n]}
It’s worth noting that:
- The product of two even signals or of two odd signals results in an even signal.
- The product of an even signal and an odd signal yields an odd signal.
5. Periodic and Nonperiodic Signals
Continuous Time Periodic Signal
A continuous-time signal x(t) is considered periodic with period T if there exists a positive nonzero value of T such that:
x(t + T) = x(t) for all t
An example of such a signal is shown below.
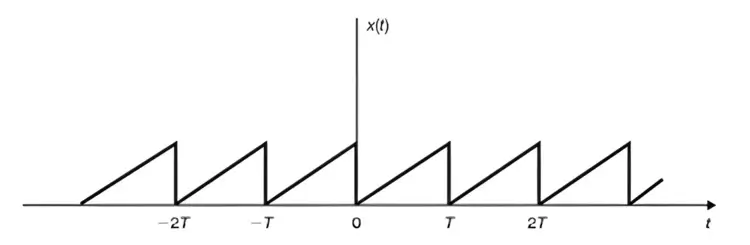
From equation x(t + T) = x(t) or figure above, it can be deduced that:
x(t + mT) = x(t) for all t and any integer m.
The fundamental period T0 of x(t) is defined as the smallest positive value of T for which equation x(t + T) = x(t) holds.
It’s essential to understand that this definition doesn’t extend to a constant signal x(t), often referred to as a DC signal. For a constant signal x(t), determining a fundamental period is not feasible because x(t) repeats indefinitely for any choice of T, rendering the concept of a smallest positive value irrelevant.
Any continuous-time signal that is not periodic is referred to as a nonperiodic (or aperiodic) signal.
Discrete Time Periodic Signal
Periodic discrete-time signals are defined similarly. A sequence (discrete-time signal) x[n] is considered periodic with period N if there exists a positive integer N such that:
x[n + N] = x[n] for all n
An example of such a sequence is illustrated in figure below.
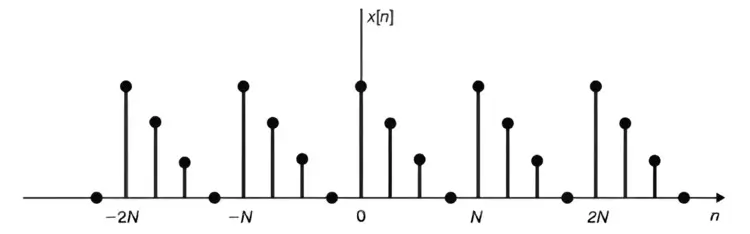
From Equation x[n + N] = x[n] and figure above, it can be concluded that:
x[n + mN] = x[n] for all n and any integer m.
The fundamental period N0 of x[n] is defined as the smallest positive integer N for which x[n + N] = x[n] holds.
Any sequence that lacks periodicity is termed a nonperiodic (or aperiodic) sequence.
It’s worth noting that
- A sequence obtained by uniformly sampling a periodic continuous-time signal may not exhibit periodicity.
- The sum of two continuous-time periodic signals may not result in a periodic signal.
- Conversely, the sum of two periodic sequences always yields a periodic sequence.
6. Energy and Power Signals
Consider v(t) to be the voltage across a resistor R producing a current i(t). The instantaneous power p(t) per ohm is defined as
p(t)= $ \frac {v(t)i(t)}{R} $ = $ i^ {2} $ (t)
Total energy E and average power P on a per-ohm basis are
E= $ \int _ {-\infty }^ {\infty } $ $ i^ {2} $ (t)dt joules
P= $ \lim _ {T\rightarrow \infty } $ $ \frac {1}{T} $ $ \int _ {-T/2}^ {T/2} $ $ i^ {2} $ (t)dt watts
For an arbitrary continuous-time signal x(t),
- The normalized energy content E of x(t) is defined as:
- E= $ \int _ {-\infty }^ {\infty } $ |x(t) $ |^ {2} $ $ dt $
- The normalized average power P is defined as:
- P= $\lim_{T\to\infty}\frac1T\int_{-T/2}^{T/2}\Bigl|x(t)\Bigr|^2dt$
Similarly, for a discrete-time signal x[n],
- The normalized energy content E is defined as:
- E= $ \sum _ {n=-\infty}^ {\infty } $ |x|n] $ ^ {2} $
- The normalized average power P is defined as:
- P= $\lim_{N\to\infty}\frac1{2N+1}\sum_{n\operatorname{=}-N}^N\left|x[n]\right|^2$
| Signal Type | Normalized Energy Content (E) | Normalized Average Power (P) |
|---|---|---|
| Continuous-time (x(t)) | E= $ \int _ {-\infty }^ {\infty } $ |x(t) $ |^ {2} $ $ dt $ | P= $\lim_{T\to\infty}\frac1T\int_{-T/2}^{T/2}\Bigl|x(t)\Bigr|^2dt$ |
| Discrete-time (x[n]) | E= $ \int _ {-\infty }^ {\infty } $ |x(t) $ |^ {2} $ $ dt $ | P= $\lim_{N\to\infty}\frac1{2N+1}\sum_{n\operatorname{=}-N}^N\left|x[n]\right|^2$ |
Based on above definitions, the following classes of signals are defined:
- x(t) (or x[n]) is considered an energy signal (or sequence) if and only if 0<E<∞, and consequently P=0.
- x(t) (or x[n]) is classified as a power signal (or sequence) if and only if 0<P<∞, thereby implying that E=∞.
- Signals that do not meet either of these conditions are referred to as neither energy nor power signals (NENP).
| Signal Type | Condition | Energy Content (E) | Average Power (P) |
|---|---|---|---|
| Energy Signal (or Sequence) | 0<E<∞ | 0<E<∞ | P=0 |
| Power Signal (or Sequence) | 0<P<∞ | E=∞ | 0<P<∞ |
| Neither Energy nor Power | E=∞ or P=∞ or both | E=∞ or P=∞ or both | E=∞ or P=∞ or both |
It’s worth noting that
- A periodic signal is classified as a power signal if its energy content per period is finite.
- In such cases, the average power of the signal only needs to be calculated over a period.
Summary
| Signal Type | Description |
|---|---|
| Continuous-time (x(t)) | Signals varying continuously over time, represented by functions of an independent variable t. |
| Discrete-time (x[n]) | Signals defined at discrete points in time, represented as sequences of numbers. |
| Analog Signal | Continuous-time signals that can take on any value in a continuous interval. |
| Digital Signal | Discrete-time signals that can only take on a finite number of distinct values. |
| Real Signal | Signals whose values are real numbers. |
| Complex Signal | Signals whose values are complex numbers. |
| Even Signal | Signals where x(-t) = x(t) (or x[-n] = x[n]). |
| Odd Signal | Signals where x(-t) = -x(t) (or x[-n] = -x[n]). |
| Periodic Signal | Signals that repeat themselves over a period of time. |
| Nonperiodic (Aperiodic) Signal | Signals that do not repeat themselves. |
| Energy Signal | Signals with finite energy content (0 < E < ∞) and zero average power (P = 0). |
| Power Signal | Signals with finite average power (0 < P < ∞) and infinite energy content (E = ∞). |
| Neither Energy nor Power Signal | Signals with infinite energy content or infinite average power, or both (E = ∞ or P = ∞ or both). |
| Sampling | The process of obtaining discrete-time signals from continuous-time signals. |
| Energy and Power Calculation | Calculating energy and average power for continuous-time and discrete-time signals, involving integration or summation. |
| Periodic Signal Power | Periodic signals can be power signals if their energy content per period is finite, and their average power is calculated over a period. |




1 thought on “Signal Classification – Types of Signals”
Comments are closed.