Definition
A signal, formally defined as a function of one or more variables, conveys information about the nature of a physical phenomenon.
In simple terms, we can define a signal as any physical quantity that changes with time, distance, speed, position, pressure, temperature, or some other quantity. Signals consist of many sinusoidal waves with different amplitudes and frequencies.
Signals transmit or carry some type of information. A signal is anything that is visible, audible, observable or measurable with the help of some machine. Examples include speech, audio, light, radio, TV, radar, supersonic, temperature, ECG, EEG, etc.
Significance of Signals in Daily Life
In one way or another, signals play a significant role in our daily lives. As an example, most people communicate with one another through the use of speech signals in face-to-face conversations or through telephone calls. The visual form of human communication is another common way of communicating, in which we send signals in the form of pictures of people or objects around us.
Yet another form of human communication is electronic mail over the Internet. In addition to providing mail, the Internet serves as a powerful medium for searching for information of general interest, for advertising, for telecommuting, for education, and for playing games. All of these forms of communication over the Internet involve the use of information-bearing signals of one kind or another. Other real-life examples in which signals of interest arise are discussed subsequently.
By listening to the heartbeat of a patient and monitoring his or her blood pressure and temperature, a doctor is able to diagnose the presence or absence of an illness or disease. The patient’s heartbeat and blood pressure represent signals that convey information to the doctor about the state of health of the patient.
When we listen to a weather forecast over the radio, we hear references to daily changes in temperature, humidity, and wind speed and direction. Using these signals, we can, for example, decide whether to stay indoors or go for a walk based on our mood.
The daily fluctuations in the prices of stocks and commodities on world markets, in their own ways, represent signals that convey information on how the shares in a particular company or corporation are doing. On the basis of this information, they make decisions regarding whether to venture into new investments or sell off old ones.
A probe exploring outer space sends valuable information about a faraway planet back to a station on Earth. The information may take the form of radar images representing surface profiles of the planet, infrared images conveying information on how hot the planet is, or optical images revealing the presence of clouds around the planet. By studying these images, our knowledge of the unique characteristics of the planet in question is enhanced significantly. Indeed, the list of what constitutes a signal is almost endless.
Types of Signal
As the definition of signal states, a signal is a function of one or more variables that conveys information about a physical phenomenon.
1. One dimensional and Multi dimensional Signals
According to the number of variables, signals can be classified into two.
1. One dimensional Signal
2. Multidimensional Signal
One dimensional
When the function depends on a single variable, we say the signal to be one dimensional.
If the signal is a function of a single independent variable, the signal called a one-dimensional signal.
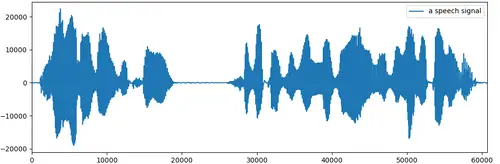
A speech signal is an example of a one-dimensional signal whose amplitude varies with time, depending on the spoken word and who speaks it.
$s_1(t)=5 t \quad$ or $\quad s_1(t)=5 t^2 \quad \Rightarrow$ one variable
Multidimensional
When the function depends on two or more variables, we say the signal to be multidimensional.
A signal called M-dimensional if its value is a function of M independent variables.
An image is an example of a two-dimensional signal, with the horizontal and vertical coordinates of the image representing the two dimensions.
$S(x, y)=3 x+4 x y+6 x^2 \quad \Rightarrow$ two variables $\mathrm{x}$ and $\mathrm{y}$
Examples of Multidimensional Signal
2-dimensional signal: The gray picture is an example of a 2-dimensional signal. The brightness or the intensity $I(x, y)$ at each point is a function of 2 independent variables.
3-dimensional signal: The black & white TV picture $[I(x, y, t)]$ : is a “3-Dimensional” since the brightness is a function of time.
Multidimensional Signal: The color TV picture is a multi-channel/multidimensional signal.
$$
I(x, y, t)=\left[\begin{array}{l}
I_r(x, y, t) \\
I_g(x, y, t) \\
I_b(x, y, t)
\end{array}\right]
$$
| One dimensional Signal | Multidimensional Signal |
|---|---|
| Function depends on a single variable | Function depends on two or more variables |
| Example: Speech Signal | Example: Image |
2. One Channel and Multi Channel Signals
Depending on the number of sources for the signals:
1.One channel signals
2.Multi channel signals
If a signal is generated from a single sensor or source, it is called a single channel signal. Example ECG signals.
- Signals are generated by multiple source or multiple sensor. This signals, can
represented in vector form. - Example: ECG (Electrocardiogram) are often used 3-channel and 12- channel
Signals generated from multiple sensors or sources or multiple signals generated from the same source are known as multi-channel signals. Multi-channel signal will be the vector sum of signals generated from multiple sources.
3. Continuous and Discrete Signals
Depending on whether the dependent variable is continuous or discrete:
1. Continuous signals
2. Discrete signals
Continues-Time Signal: A signal x(t) is said to be a continuous time signal if it is defined for all time t. A continuous signal is specified at every value of its independent variable. For example, the temperature of a room is a continuous signal.
Discrete-Time Signal: A discrete time signal x[nT] has values specified only at discrete points in time. The important advantage of discrete signals is that they can be stored and processed efficiently using digital devices and fast numerical algorithms.
As most practical signals are continuous signals, the discrete signal is often obtained by sampling the continuous signal. However, signals such as yearly population of a country and monthly sales of a company are inherently discrete signals.
Study more about them here: Continuous Time Signal, Discrete Time Signal and Digital Signal
4. Analog and Digital Signals
If a continuous-time signal $x(t)$ can take on any value in the continuous interval $(a, b)$, where $a$ may be $-\infty$ and $b$ may be $+\infty$, then the continuous-time signal $x(t)$ is called an analog signal.
If a discrete-time signal $x[n]$ can take on only a finite number of distinct values, then we call this signal a digital signal.
5. Real and Complex Signals
A signal x(t) is a real signal if its value is a real number, and a signal x(t) is a complex signal if its value is a complex number.
A general complex signal x(t) is a function of the form
$$x(t)=x_1(t)+j x_2(t)$$
6. Deterministic and Random Signals
Deterministic signals are those signals whose values are completely specified for any given time. Thus, a deterministic signal can be modeled by a known function of time t.
Random signals are those signals that take random values at any given time and must be characterized statistically.
7. Even and Odd Signals
A signal $x(t)$ pr $x[n]$ is referred to as an even signal if
$$
\begin{aligned}
x(-t) &=x(t) \\
x[-n] &=x[n]
\end{aligned}
$$
A signal $x(t)$ or $x[n]$ is referred to as an odd signal if
$$
\begin{aligned}
&x(-t)=-x(t) \\
&x[-n]=-x[n]
\end{aligned}
$$
Representation of Signals
Mathematically, a signal is represented as a function of an independent variable t. Usually, t represents time. Thus, a signal is denoted by x(t).
We denote a continuous signal, using the independent variable t, as x(t). We call this representation the time-domain representation, although the independent variable is not time for some signals.
A discrete signal is specified only at discrete values of its independent variable. For example, a signal x(t) is represented only at t = nTs as x(nTs), where Ts is the sampling interval and n is an integer. The discrete signal is usually denoted as x(n), suppressing Ts in the argument of x(nTs).