Definition: The magnetomotive force (MMF) is defined as the work done in moving a unit magnetic pole once around the magnetic circuit. It is measured in ampere-turns.
Magnetomotive force (MMF) is like the pressure that makes magnetic flux happen in a magnetic circuit. Without MMF, there can’t be any flux in the magnetic circuit. MMF in a magnetic circuit is similar to electromotive force in an electric circuit.
What is Magnetomotive Force?
The product of current and turns, known as IN, denotes the magnetizing force or magnetic potential, termed as magnetomotive force (mmf).
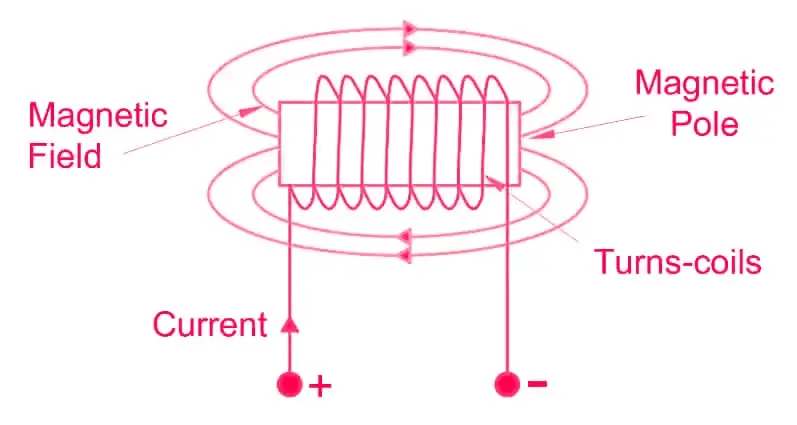
The magnetic field strength of a coil magnet is influenced by the amount of current flowing through its turns.
More current flowing through the coil leads to a stronger magnetic field. Additionally, having more turns in a specific length concentrates the magnetic field.
The coil, resembling a bar magnet, possesses opposite poles at its ends, resulting in a magnetic field proportional to the ampere-turns.
The magnetomotive force (MMF) drives or tends to drive flux through a magnetic circuit and corresponds to electromotive force (EMF) in an electric circuit. Magnetomotive force is equal to the work done in joules in carrying a unit magnetic pole once through the entire magnetic circuit.
In fact, as potential difference between any two points is measured by the work done in carrying a unit charge from one points to another, similarly, mmf between two points is measured by the work done in joules in carrying a unit magnetic pole from one point to another.
MMF Equation
This relationship is expressed as:
MMF = Current (I) × Number of Turns (N)
where I is the current in amperes and N is number of turns.
Practical Unit: Ampere-turn
The practical unit for measuring magnetomotive force is the ampere-turn, abbreviated as AT. This unit reflects the combined effect of current and turns in a coil.
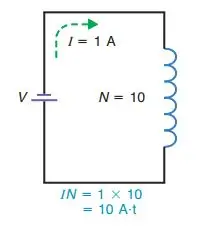
MMF = N x I = 10 x 1 = 10 AT
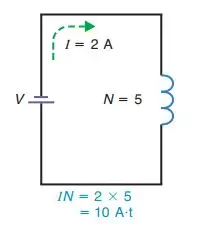
MMF = N x I = 5 x 2 = 10 AT
Two examples of equal ampere-turns for the same mmf are shown above. A solenoid with 5 turns and 2 amperes exhibits the same magnetizing force as one with 10 turns and 1 ampere, as the product of amperes and turns remains consistent.
Utilizing thinner wire allows for more turns to be accommodated within a given space, influencing the magnetic field strength. The amount of current flowing through the coil depends on the wire’s resistance and the source voltage.
The required number of ampere-turns depends on the desired magnetic field strength. Adjustments in current or turns can be made accordingly.
Units of Magnetomotive Force
The ampere-turn, AT, is an SI unit. It is calculated as NI with the current in amperes.
The cgs unit of mmf is the gilbert, abbreviated Gb.
One ampere-turn equals 1.26 Gb. The number 1.26 is approximately 4π/10, derived from the surface area of a sphere, which is 4πr2.
To convert IN to gilberts, multiply the ampere-turns by the constant conversion factor 1.26G/1 AT.
As an example, 1000 AT is the same mmf as 1260 Gb. The calculations are 1000 AT × 1.26 Gb/1 AT = 1260 Gb. Note that the units of AT cancel in the conversion.
| Description | Information |
|---|---|
| Ampere-turn (AT) | SI unit for magnetomotive force |
| Calculation | AT = I × N |
| cgs unit of mmf | Gilbert (Gb) |
| Conversion factor | 1 AT = 1.26 Gb |
| Conversion to gilberts | Multiply AT by 1.26 Gb |
| Example conversion | 1000 AT = 1260 Gb |
Solved Example Problems
Example 1
Calculate the ampere-turns of mmf for a coil with 2000 turns and a 5-mA current.
Solution:
To calculate the ampere-turns (AT) of magnetomotive force (mmf) for a coil with 2000 turns and a 5-mA (0.005 A) current, we can use the formula:
$\text{AT} = I \times N $
Where:
- ( I ) = Current in amperes
- ( N ) = Number of turns
Given:
- I = 0.005 A
- N = 2000 turns
Substituting the values:
$\text{AT} = 0.005 \, \text{A} \times 2000 \, \text{turns} $
$ \text{AT} = 10 \, \text{A-turns} $
So, the ampere-turns of mmf for the given coil is 10 A-turns.
Example 2
To find the number of turns required for a coil to provide a magnetizing force of 600 A?t with a current of 4 A, we can rearrange the formula for ampere-turns:
$ \text{AT} = I \times N $
Given:
- AT = 600 ) AT
- I = 4 A
We rearrange the formula to solve for ( N ):
$ N = \frac{\text{AT}}{I} $
Substituting the given values:
$ N = \frac{600 \, \text{A?t}}{4 \, \text{A}} $
$ N = 150 \, \text{turns} $
Therefore, 150 turns are necessary for the coil to provide a magnetizing force of 600 AT with a current of 4 A.