Here are a collection of DC motor problems and solution. You can find problems on various topics related to dc motor such as types of dc motors, speed control of dc motor, torque of dc motor, characteristics of dc motor etc.
DC Motor Problem 1
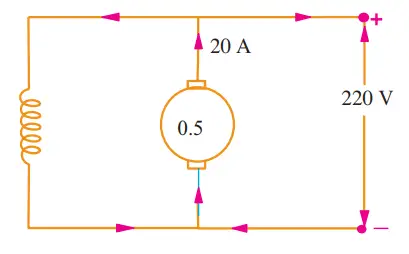
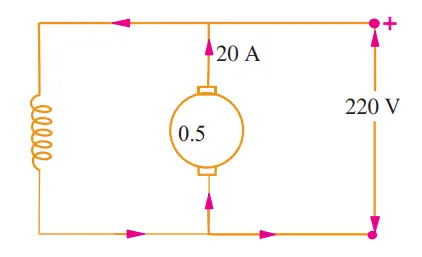
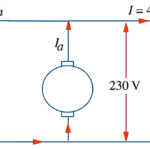
A 220-V d.c. machine has an armature resistance of 0.5 Ω. If the full-load armature current is 20 A, find the induced e.m.f. when the machine acts as (i) generator (ii) motor.
Solution:
To find the induced EMF in a 220-V DC machine with an armature resistance of 0.5 Ω and a full-load armature current of 20 A, we need to consider the machine operating both as a generator and as a motor.
Given Data:
- Voltage, $ V = 220 \, \text{V} $
- Armature resistance, $ R_a = 0.5 \, \Omega $
- Full-load armature current, $ I_a = 20 \, \text{A} $
(i) When the machine acts as a generator:
In a generator, the terminal voltage $ V $ is given by:
$$ V = E_g – I_a R_a $$
Where $ E_g $ is the induced EMF in the generator.
Rearrange the equation to solve for $ E_g $:
$$ E_g = V + I_a R_a $$
Substitute the known values:
$ E_g = 220 \, \text{V} + 20 \, \text{A} \times 0.5 \, \Omega $
$ E_g = 220 \, \text{V} + 10 \, \text{V} $
$ E_g = 230 \, \text{V} $
Therefore, the induced EMF when the machine acts as a generator is 230 V.
(ii) When the machine acts as a motor:
In a motor, the terminal voltage $ V $ is given by:
$$ V = E_b + I_a R_a $$, Where $ E_b $ is the back EMF in the dc motor.
Rearrange the equation to solve for $ E_b $:
$$ E_b = V – I_a R_a $$
Substitute the known values:
$ E_b = 220 \, \text{V} – 20 \, \text{A} \times 0.5 \, \Omega $
$ E_b = 220 \, \text{V} – 10 \, \text{V} $
$ E_b = 210 \, \text{V} $
Therefore, the induced EMF when the machine acts as a motor is 210 V.
DC Motor Problem 2
A DC motor takes an armature current of 110 A at 480 V. The armature circuit resistance is 0.2 Ω. The machine has 6-poles and the armature is lap-connected with 864 conductors. The flux per pole is 0.05 Wb. Calculate (i), the speed and (ii) the gross torque developed by the armature.
Solution:
To calculate the speed and the gross torque developed by the armature of the DC motor, we will use the given parameters:
- Armature current, $ I_a = 110 \text{ A} $
- Armature voltage, $ V = 480 \text{ V} $
- Armature resistance, $ R_a = 0.2 \, \Omega $
- Number of poles, $ P = 6 $
- Number of conductors, $ Z = 864 $
- Flux per pole, $ \Phi = 0.05 \text{ Wb} $
- Type of winding: lap-connected
(i) Speed of the Motor
Calculate the Back EMF $ E_b $:
The back EMF $ E_b $ can be calculated using the voltage equation of the motor:
$$E_b = V – I_a R_a$$
Substituting the given values:
$E_b = 480 \text{ V} – (110 \text{ A} \times 0.2 \, \Omega)$
$E_b = 480 \text{ V} – 22 \text{ V} = 458 \text{ V}$
Calculate the Speed $ n $ in RPM:
The back EMF for a lap-wound motor is given by:
$$E_b = \frac{P \Phi Z n}{60 A}$$
Where:
- $ P $ = Number of poles
- $ \Phi $ = Flux per pole in Weber
- $ Z $ = Total number of conductors
- $ n $ = Speed in RPM
- $ A $ = Number of parallel paths (For lap winding, $ A = P $)
Rearrange to solve for $ n $:
$$n = \frac{E_b \times 60 \times A}{P \times \Phi \times Z}$$
Substitute the values:
$n = \frac{458 \text{ V} \times 60 \times 6}{6 \times 0.05 \text{ Wb} \times 864}$
Simplify the equation:
$n = \frac{458 \times 60}{0.05 \times 864}$
$n \approx 636.11 \text{ RPM}$
Therefore, the speed of the motor is approximately 636.11 RPM.
(ii) Gross Torque Developed by the Armature
The torque $ T $ developed by the armature can be calculated using the power equation:
$$P_{mech} = T \cdot \omega$$
Where $ P_{mech} $ is the mechanical power in watts and $ \omega $ is the angular speed in radians per second.
First, convert the speed from RPM to rad/s:
$$\omega = \frac{2 \pi n}{60}$$
Substituting $ n = 636.11 $:
$\omega = \frac{2 \pi \times 636.11}{60} \approx 66.66 \text{ rad/s}$
The electrical power converted to mechanical power by the armature (neglecting losses other than armature resistance) is given by:
$$P_{mech} = E_b \times I_a$$
Substituting the known values:
$$P_{mech} = 458 \text{ V} \times 110 \text{ A} = 50380 \text{ W}$$
Now, solve for the torque:
$T = \frac{P_{mech}}{\omega} = \frac{50380 \text{ W}}{66.66 \text{ rad/s}}$
$ T = \approx 755.85 \text{ Nm}$
Therefore, the gross torque developed by the armature is approximately 755.85 Nm.
DC Motor Problem 3
A 250-V, 4-pole, wave-wound DC series motor has 782 conductors on its armature. It has armature and series field resistance of 0.75 ohm. The motor takes a current of 40 A. Estimate its speed and gross torque developed if it has a flux per pole of 25 mWb.
Solution:
Calculate Back EMF ((E_b)):
$E_b = V – I_a(R_a + R_{series})$
$E_b = 250 \, \text{V} – 40 \, \text{A} \times (0.75 \, \Omega + 0.75 \, \Omega)$
$E_b = 250 \, \text{V} – 60 \, \text{V} = 190 \, \text{V}$
Calculate Speed ((n)):
$$n = \frac{E_b \times 60 \times 2}{P \times \Phi \times Z}$$
$n = \frac{190 \, \text{V} \times 60 \times 2}{4 \times 25 \, \text{mWb} \times 782}$
$n = \frac{22800}{782} \approx 29.17 \, \text{RPM}$
Convert RPM to rad/s:
$$\omega = \frac{2 \pi \times 29.17}{60} \approx 3.05 \, \text{rad/s}$$
Calculate Gross Torque ((T)):
$$P_{mech} = E_b \times I_a$$
$P_{mech} = 190 \, \text{V} \times 40 \, \text{A} = 7600 \, \text{W}$
$T = \frac{P_{mech}}{\omega} = \frac{7600 \, \text{W}}{3.05 \, \text{rad/s}} $
$T \approx 2491.8 \, \text{Nm}$
Therefore, the speed of the motor is approximately 29.17 RPM, and the gross torque developed by the armature is approximately 2491.8 Nm.
DC Motor Problem 4
A 400 V DC motor takes an armature current of 100 A when its speed is 1000 rpm If the armature
resistance is 0·25 ohm, calculate the torque produced in Nm.
Solution:
Sure, here are the equations in (\LaTeX) format:
- Calculate the back EMF (($E_b$)):
$$
E_b = V – I_a R_a
$$
- Calculate the mechanical power output (($P_{\text{mech}}$)):
$$
P_{\text{mech}} = E_b \times I_a
$$
- Calculate the angular speed (($\omega$)):
$$
\omega = \frac{2 \pi N}{60}
$$
- Calculate the torque (($T$)):
$$
T = \frac{P_{\text{mech}}}{\omega}
$$
Putting all the calculations together:
$$
E_b = 400\,\text{V} – (100\,\text{A} \times 0.25\,\Omega) = 400\,\text{V} – 25\,\text{V} = 375\,\text{V}
$$
$$
P_{\text{mech}} = 375\,\text{V} \times 100\,\text{A} = 37500\,\text{W}
$$
$$
\omega = \frac{2 \pi \times 1000}{60} \approx 104.72\,\text{rad/s}
$$
$$
T = \frac{37500\,\text{W}}{104.72\,\text{rad/s}} \approx 358.13\,\text{Nm}
$$
Thus, the torque produced by the motor is approximately 358.13 Nm.


THANK YOU FOR HELPING ME. I REALY APPRECIATE YOUR WORK