Have you ever wondered how combination of capacitors work together in electronic circuits? Well, understanding how capacitors are grouped and connected is really important. It helps us use them effectively in our gadgets and devices.
In this article, we’ll explore why we combine capacitors and how we connect them. We’ll also look at the two main ways we can connect capacitors: in parallel and in series. By the end, you’ll see how these connections affect the overall capacitance and voltage in a circuit. And don’t worry, we’ll wrap up by solving some problems based on combination of capacitors. So, if you’re curious about how capacitors team up to make electronics work, stick around!
Methods of Combination of Capacitors
Necessity of capacitor combination : In certain instances, we may not be able to get a required value of capacitance and a required voltage rating. In such instances, to get the required capacitances from the available capacitors and to give only the safe voltage across capacitor, the capacitors have to be grouped in different fashions. Such combination of capacitors is very essential.
There are two methods of combination of capacitors
- Parallel Combination
- Series Combination
Parallel Combination of Capacitors
Capacitors are connected in parallel combination to achieve a higher capacitance than what is available in one unit.
Conditions for parallel grouping
- Voltage rating of capacitors should be higher than the supply voltage Vs.
- Polarity should be maintained in the case of polarised capacitors (electrolytic capacitors).
Total capacitance in Parallel Combination
Parallel grouping of capacitors is shown below and is analogous to the connection of resistance in parallel or cells in parallel.
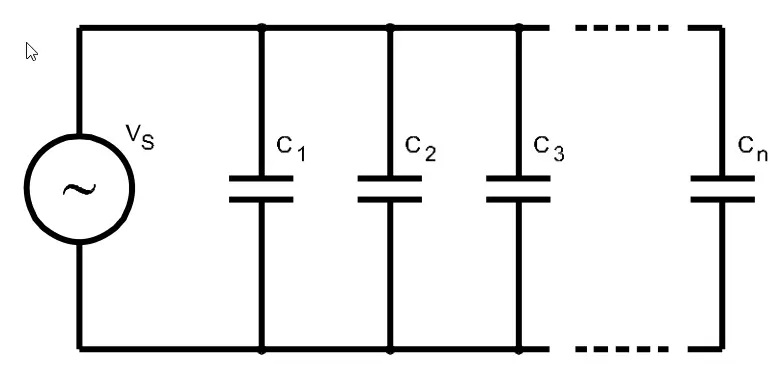
When capacitors are connected in parallel, the total capacitance is the sum of the individual capacitances, because the effective plate area increases.
The calculation of total parallel capacitance is analogous to the calculation of total resistance of a series circuit.
Parallel combination of capacitances increases the effective plate area. This is explained in the pictures below.
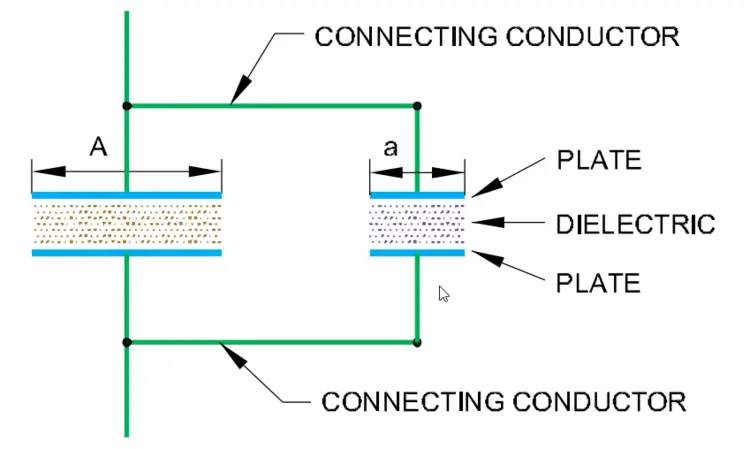
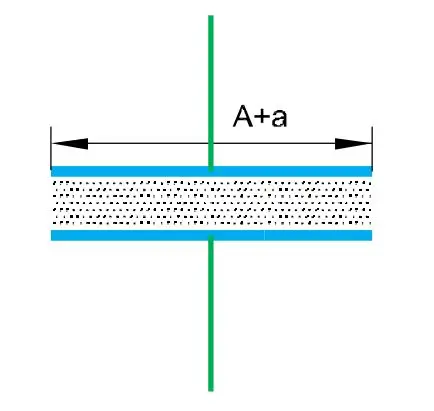
From the above figures, you can understand that connecting capacitors in parallel effectively increases the plate area. Plate are of the two capacitors are A and a but the plate area of the equivalent capacitance of the parallel combination is the sum of the two A+a.
General formula for parallel capacitance
The total capacitance of parallel capacitors is found by adding the individual capacitances.
CT = C1 + C2 + C3 +………….+ Cn
where CT is the total capacitance,
C1 , C2 , C3 etc. are the parallel capacitors.
The voltage applied to a parallel group must not exceed the lowest breakdown voltage for all the capacitors in the parallel group.
Example:
Suppose three capacitors are connected in parallel, where two have a breakdown voltage of 250 V and one has a breakdown voltage of 200 V, then the maximum voltage that can be applied to the parallel group without damaging any capacitor is 200 volts.
The voltage across each capacitor will be equal to the applied voltage.
Charge stored in parallel grouping
Since the voltage across parallel-grouped capacitors is the same, the larger capacitor stores more charge. If the capacitors are equal in value, they store an equal amount of charge. The charge stored by the capacitors together equals the total charge that was delivered from the source.
QT= Q1+ Q2 + Q3+…..+ Qn
where QT is the total charge
Q1, Q2, Q3…..etc. are the individual charges of the capacitors in parallel.
Using the equation Q = CV, the total charge QT = CTVS
where VS is the supply voltage.
CTVS = C1VS + C2VS + C3VS
Because all the VS terms are equal, they can be cancelled.
∴ CT = C1 + C2 + C3
Series Combination of Capacitors
The necessity of grouping capacitors in series is to reduce the total capacitance in the circuit.
Another reason is that two or more capacitors in series can withstand a higher potential difference than an individual capacitor can. But, the voltage drop across each capacitor depends upon the individual capacitance.
If the capacitances are unequal, you must be careful not to exceed the breakdown voltage of any capacitor.
Conditions for Series Combination
- If different voltage rating capacitors have to be connected in series, take care to see that the voltage drop across each capacitor is less than its voltage rating.
- Polarity should be maintained in the case of polarised capacitors.
Total Capacitance in Series Combination
Series combination of capacitors is shown in the figure below
When capacitors are connected in series, the total capacitance is less than the smallest
capacitance value, because
- the effective plate separation thickness increases
- and the effective plate area is limited by the smaller plate.
The calculation of total series capacitance is analogous to the calculation of total resistance of parallel resistors.
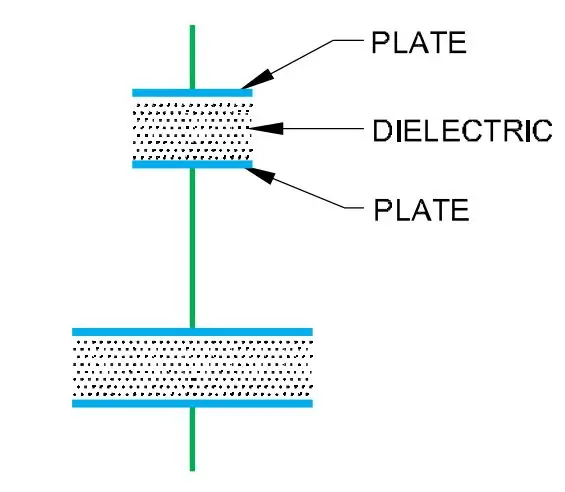
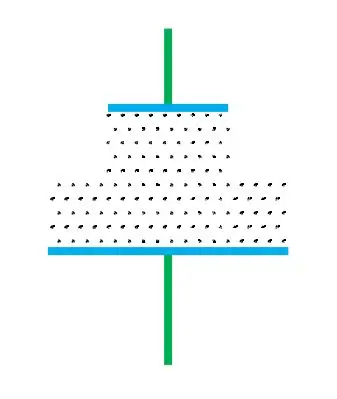
By comparing the two figures above you can understand that connecting capacitors in series increases the plate separation thickness, and also limits the effective area so as to equal that of the smaller plate capacitor.
General formula for series capacitance:
The total capacitance of the series capacitors can be calculated by using the formula
$$\mathrm{C_T=\frac1{\frac1{C_1}+\frac1{C_2}+\frac1{C_3}+………+\frac1{C_n}}}$$
or $$\frac1{\mathrm{C_T}}=\frac1{\mathrm{C_1}}+\frac1{\mathrm{C_2}}+\frac1{\mathrm{C_3}}+…….+\frac1{\mathrm{C_n}}$$
- If there are two capacitors in series, $C_T=\frac{C_1C_2}{C_1+C_2}$
- If there are three capacitors in series, $C_T=\frac{C_1C_2C_3}{(C_1C_2)+(C_2C_3)+(C_3C_1)}$
- If there are `n’ equal capacitors in series, $\mathrm{C}_\mathrm{T}=\frac{\mathrm{C}}{\mathrm{n}}$
Maximum voltage across each capacitor
In series combination of capacitors, the division of the applied voltage among the capacitors depends on the individual capacitance value according to the formula
C = Q/V
The largest value capacitor will have the smallest voltage because of the reciprocal relationship. Likewise, the smallest capacitance value will have the largest voltage.
The voltage across any individual capacitor in a series connection can be determined using the following formula.
$$\mathrm{V_X=\frac{C_T}{C_X}\times V_S}$$
where Vx – individual voltage of each capacitor
Cx – individual capacitance of each capacitor
Vs – supply voltage.
The potential difference does not divide equally if the capacitances are unequal. If the capacitances are unequal you must be careful not to exceed the breakdown voltage of any capacitor.
Solved Problems of Combination of Capacitors
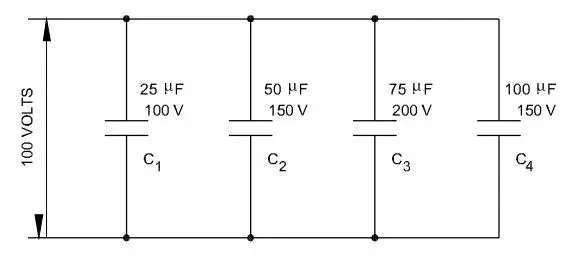
Problem 1: Calculate the total capacitance, individual charges and the total charge of the circuit given in the figure below.
Solution:
Total capacitance = CT
CT = C1 + C2 + C3+C4
CT = 25+50+75+100 = 250 micro farads.
Total Charge = QT = Q1+ Q2 + Q3+ Q4
Q1 = C1V = 25 x 100 x 10–6 = 2500 x 10–6 = 2.5 x 10–3 coulombs.
Q2 = C2V = 50 x 100 x 10–6 = 5000 x 10–6 = 5 x 10–3 coulombs.
Q3 = C3V = 75 x 100 x 10–6 = 7500 x 10–6 = 7.5 x 10-3 coulombs.
Q4 = C4V = 100 x 100 x 10-6 = 10000 x 10-6 = 10 x 10-3 coulombs.
Total Charge = QT = Q1+ Q2 + Q3+ Q4
QT = 2.5 x 10–3 + 5 x 10–3 + 7.5 x 10-3 + 10 x 10-3
QT = 25 x 10-3 coulombs.
or QT = CT V = 250 x 10-6 x 100 = 25 x 10-3 coulombs.
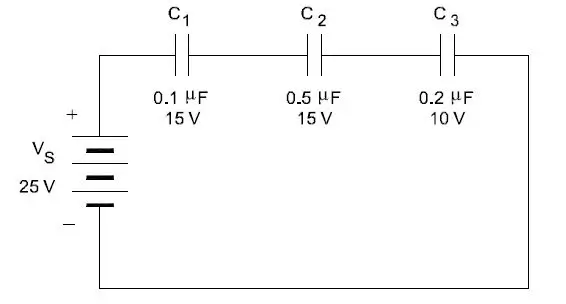
Problem 2: Find the voltage across each capacitor in the figure below.
Solution:
$$\mathrm{C_T=\frac1{\frac1{C_1}+\frac1{C_2}+\frac1{C_3}+………+\frac1{C_n}}}$$
$$\frac1{C_{\mathrm{T}}}=\frac1{0.1}+\frac1{0.5}+\frac1{0.2}$$
$$\frac{1}{C_{T}}=\frac{10}{1}+\frac{2}{1}+\frac{5}{1}$$
CT = 0.0588 micro farad
$\mathrm{V_1=\frac{C_T}{C_1}\times V_S}$ = 14.71 volts
$\mathrm{V_2=\frac{C_T}{C_2}\times V_S}$ = (0.0588 / 0.5) x 25 = 2.94 volts
$\mathrm{V_3=\frac{C_T}{C_3}\times V_S}$ = (0.0588 / 0.2) x 25 =7.35 volts