This set of DC Generator Problems with Solution focuses on problems based on Types of DC Generator.
DC Generator Problem 1
A shunt generator delivers 450 A at 230 V and the resistance of the shunt field and armature are 50 Ω and 0.03 Ω respectively. Calculate the generated EMF?
DC Generator Problem 1 Solution:
The Generator Circuit is as shown in the figure,
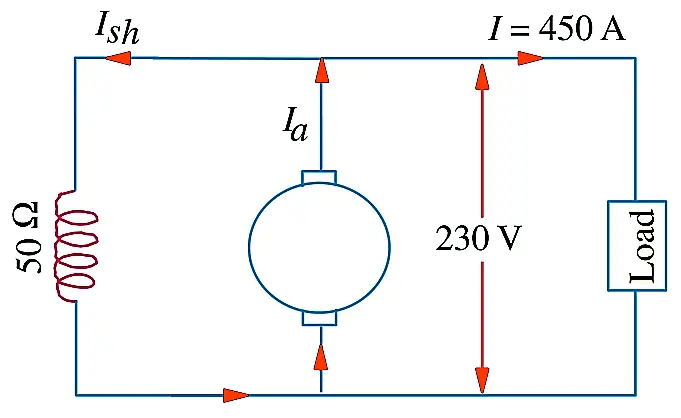
Current through shunt field winding is,
$$
\begin{aligned}
I_{\text {sh }} &=230 / 50=4.6 \mathrm{~A} \\
\text { Load current, } I &=450 \mathrm{~A} \\
\therefore \text { Armature Current } I_{a} &=I+I_{\text {sh }} \\
&=450+4.6=454.6 \mathrm{~A} \\
\text { Armature Voltage Drop, } I_{a} R_{a} &=454.6 \times 0.03 \\
&=13.6 \mathrm{~V} \\
\text { Now, Generated Emf, } E_{g} &=\text { terminal voltage }+\text { armature drop } \\
&=V+I_{a} R_{a} \\
\therefore \text { Emf generated in armature } & \\
E_{g} &=230+13.6 \\
&=243.6 \mathrm{~V}
\end{aligned}
$$
DC Generator Problem 2
A four pole generator having wave-wound armature winding has 51 slots, each slot containing 20 conductors. What will be the voltage generated in the machine when driven at 1500 rpm assuming the flux per pole to be 7.0 mWb ?
DC Generator Problem 2 Solution:
For a simplex wave wound generator,
The formula to calculate the generated voltage of a DC generator is:
E = (P * Z * N * Φ) / (60 * A)
where:
E = generated voltage in volts (V)
P = number of poles
Z = total number of armature conductors
N = speed of the generator in revolutions per minute (RPM)
Φ = flux per pole in webers (Wb)
A = number of parallel paths in the armature winding
In this case, we have:
P = 4 (four poles)
Z = 51 slots x 20 conductors/slot = 1020 armature conductors
N = 1500 RPM
Φ = 7.0 mWb = 7.0 x 10-3 Wb
A = 2 (wave-wound armature winding)
Substituting these values into the formula, we get:
E = (4 * 1020 * 1500 * 7.0 x 10^-3) / (60 * 2)
E = 357 V
Therefore, the generated voltage of the four pole generator with a wave-wound armature winding, 51 slots each containing 20 conductors, and a flux per pole of 7.0 mWb when driven at 1500 RPM is 357 volts.
DC Generator Problem 3
A long-shunt compound generator delivers a load current of 50 A at 500 V and has armature, series field and shunt field resistances of 0.05 Ω, 0.03 Ω and 250 Ω respectively. Calculate the generated voltage and the armature current. Allow 1 V per brush for contact drop.
DC Generator Problem 3 Solution:
Generator circuit is shown in figure
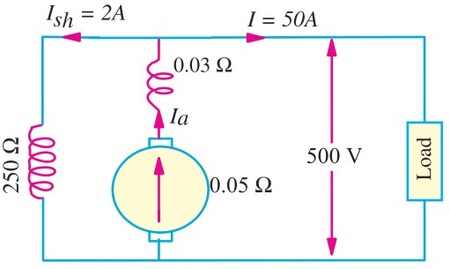
Current through shunt field winding, Ish= 500/250 = 2 A
Current through armature and series winding = 50 + 2 = 52 A
Voltage drop on series field winding = 52×0.03 = 1.56 V
Armature voltage drop, IaRa = 52×0.05 = 2.6 V
Drop at brushes = 2×1 = 2 V
Now Emf generated in armature, Eg = V + IaRa+ series drop + brush drop
= 500 + 2.6 + 1.56 + 2 = 506.16 V
DC Generator Problem 4
A short-shunt compound generator delivers a load current of 30 A at 220 V, and has armature, series-field and shunt-field resistances of 0.05 Ω, 0.30 Ω and 200 Ω respectively. Calculate the induced emf and the armature current. Allow 1.0 V per brush for contact drop.
DC Generator Problem 4 Solution:
A Short Shunt Compound Wound Generator is a type of dc generator in which the shunt field winding is connected in parallel with the armature winding only.
The circuit diagram of short-shunt compound generator mentioned in the problem is given below
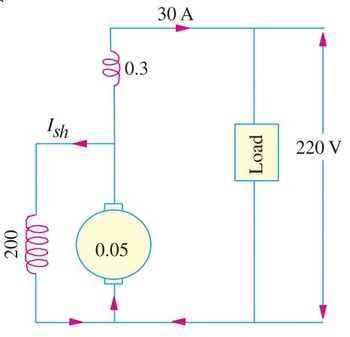
Voltage drop in series winding = 30 × 0.3 = 9 V
Voltage across shunt winding = 220 + 9 = 229 V
Ish = 229/200 = 1.145 A
Ia = 30 + 1.145 = 31.145 A
IaRa = 31.145 × 0.05 = 1.56 V
Brush drop = 2 × 1 = 2 V
Eg = V + series drop + brush drop + IaRa
= 220 + 9 + 2 + 1.56 = 232.56 V
DC Generator Problem 5
In a long-shunt compound generator, the terminal voltage is 230 V when generator delivers 150 A. Determine
(i) induced emf
(ii) total power generated
(iii) distribution of this power.
Given that shunt field, series field, divertor and armature resistance are 92 Ω, 0.015 Ω, 0.03 Ω and 0.032 Ω respectively.
DC Generator Problem5 Solution:
Ish = 230/92 = 2.5 A
Ia = 150 + 2.5 = 152.5 A
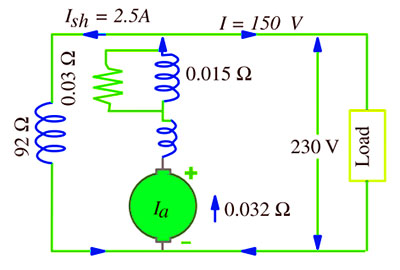
Since series field resistance and divertor resistances are in parallel their combined resistance is = 0.03 × 0.015/0.045 = 0.01 Ω
Total armature circuit resistance is = 0.032 + 0.01 = 0.042 Ω
Voltage drop = 152.5 × 0.042 = 6.4 V
(i) Voltage generated by armature, Eg = 230 + 6.4 = 236.4 V
(ii) Total power generated in armature, EgIa = 236.4 × 152.5 = 36,051 W
(iii) Power distribution
Power lost in armature IaRa = 152.52 × 0.032 = 744 W
Power lost in series field and divertor = 152.52 × 0.01 = 232 W
Power dissipated in shunt winding = VIsh = 230 × 0.01 = 575 W
Power delivered to load = 230 × 150 = 34500 W
Total = 36051 W
DC Generator Problem 6
The following information is given for a 300-kW, 600-V, long-shunt compound generator : Shunt field resistance = 75 Ω, armature resistance including brush resistance = 0.03 Ω, commutating field winding resistance = 0.011 Ω, series field resistance = 0.012 Ω, divertor resistance = 0.036 Ω. When the machine is delivering full load, calculate the voltage and power generated by the armature
DC Generator Problem 6 Solution:
Power output = 300,000 W
Output current = 300,000/600 = 500 A
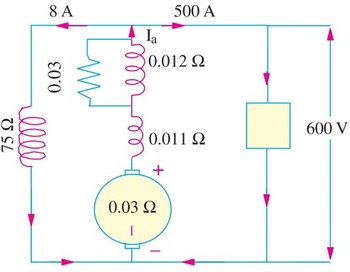
Ish = 600/75 = 8 A,
Ia= 500 + 8 = 508 A
Since the series field resistance and divertor resistance are in parallel, their combined resistance is = (0.012 × 0.036) / 0.048 = 0.009 Ω
Total armature circuit resistance = 0.03 – 0.011 + 0.009 = 0.05 Ω
Voltage drop = 508 × 0.05 = 25.4 V
Voltage generated by armature = 600 + 25.4 = 625.4 V
Power generated = 625.4 × 508 = 317,700 W = 317.7 kW
More: DC Generator Problems and Solution: EMF Equation of DC Generator

Excellent
How you say that excellent
Whenever totally are wrong process
In dc generator wave wound:- Number of poles is not is equal to number of parallel path.
Always A=2
Or,
In lap wound A=mP. Where,
(A=no. of parallel path)
(m=no. of winding)
(P=no. of poles)
I think it may be right…..
Nice explanation.
Deduce the internal characteristics from the external characteristics and estimate the full load voltage drop due to armature reaction
reply,
please
https://studyelectrical.com/2014/08/characteristics-of-shunt-generator.html
In second question u should take A=2 not 4 please make sure that
357 volts is the correct ans.
A=2 in wave wound dc generator
I like so much
Thanks for share the information in this website and your content is vert good