Percentage reactance of power system elements such as generator, transformer and reactor are extensively used in short circuit calculation when any fault occurs in the system.
Most faults in the power system lead to a short-circuit condition. When such a condition occurs, a heavy current (called short circuit current) flows through the equipment, causing considerable damage to the equipment and interruption of service to consumers.
The short circuit current in the system is limited by the impedance of the equipment connected to the system up to the point of fault.
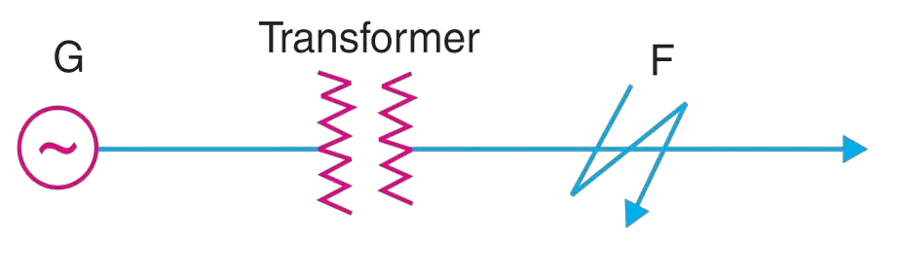
If a fault occurs on the feeder at point F, then the short circuit current from the generating station will have a value limited by the impedance of the generator and transformer and the impedance of the line between the generator and the point of fault. This shows that knowledge of the impedances of various equipment and circuits in the system is essential for the determination of short-circuit currents.
In order to make the short circuit calculation faster, the reactance of generators, transformers, and reactors is usually expressed in percentage reactance.
Read: Percentage impedance of transformer
Percentage Reactance Definition and Equation
The percentage reactance of a circuit is defined as the percentage of the total phase voltage dropped in the circuit when full-load current is flowing through it.
$$
\begin{aligned}
\% X & =\frac{I X}{V} \times 100 \\
I & =\text { full-load current } \\
V & =\text { phase voltage } \\
X & =\text { reactance in ohms per phase }
\end{aligned}
$$
Thus percentage reactance of a transformer is the percentage of phase voltage drop when full load current flows through it.
Alternatively, percentage reactance (%X) can also be expressed in terms of kVA and kV as under :
$$
X=\frac{(\% X) V}{100 I}=\frac{(\% X) V \times V}{100 \times V I}=\frac{(\% X)\left(\frac{V}{1000}\right)\left(\frac{V}{1000}\right) \times 1000}{100 \times\left(\frac{V}{1000}\right) \times I}=\frac{(\% X)(\mathrm{kV})^2 \times 10}{\mathrm{kVA}}
$$
$$
\% X=\frac{(\mathrm{kVA}) X}{10(\mathrm{kV})^2}
$$ where X is the reactance in ohms.
If X is the only reactance element in the circuit, then short-circuit current is given by ;
$$
\begin{aligned}
I_{S C} & =\frac{V}{X} \\
& =I \times\left(\frac{100}{\% X}\right)
\end{aligned}
$$
i.e. short circuit current is obtained by multiplying the full-load current by 100/% X.
Example:
If the percentage reactance of an transformer is 20% and the full-load current is 50 A.
Then short-circuit current will be 50 × 100/20 = 250 A when only that transformer is in the circuit.
Advantages of Percentage Reactance over Ohmic Reactance?
It may be worthwhile to mention here the advantage of using percentage reactance instead of ohmic reactance in short-circuit calculations. Percentage reactance values remain unchanged as they are referred through transformers, unlike ohmic reactances which become multiplied or divided by the square of transformation ratio. This makes the procedure simple and permits quick calculations.
- Percentage reactance permit rapid short circuit calculations
- Easy to remember and use: 13200V+/-1350 +/-2725 V is harder that 13200V +/ – 2.5% +/— 5%
- Enables comparation and estimation of machines independently of operation voltages and currents: small distribution transformers have Xd=ucc = 3/4%, and increases with Voltage and power. 132kV transformers have 11/15% reactance.
- Enables calculation on power systems avoiding transformer ratios, using the per-unit system, by example on short circuit calculations.
Percentage Reactance and Base kVA
From expression $\% X=\frac{(\mathrm{kVA}) X}{10(\mathrm{kV})^2}$, it is clear that percentage reactance of an equipment depends upon its kVA rating.
Generally, the various equipments used in the power system have different kVA ratings. Therefore, it is necessary to find the percentage reactances of all the elements on a common kVA rating. This common kVA rating is known as base kVA.
The value of this base kVA is quite unimportant and may be:
- equal to that of the largest plant
- equal to the total plant capacity
- any arbitrary value
The conversion can be effected by using the following relation :
$$
\% \text { age reactance at base } \mathrm{kVA}=\frac{\text { Base } \mathrm{kVA}}{\text { Rated } \mathrm{kVA}} \times \% \text { age reactance at rated } \mathrm{kVA}
$$
Thus, a 1000 kVA transformer with 5% reactance will have a reactance of 10% at 2000 kVA base






Comments are closed.