All Day Efficiency of Transformer

Table of Contents

Definition

The ratio of output in kWh to the input in kWh of a transformer over a 24-hour period is known as all day efficiency.

η_all-day = Output in kWh for 24 hrs / Input in kWh for 24 hours

All day efficiency is also known as energy efficiency.

Importance of All Day Efficiency

The ordinary or commercial efficiency of a transformer is defined as the ratio of output power to the input power.

Commercial efficiency = Output power ∕ Input power

There are certain types of transformers whose performance cannot be judged by commercial efficiency.

For instance, distribution transformers used for supplying lighting loads have their primaries energized all the 24 hours in a day but the secondaries supply little or no load during the major portion of the day.

It means that a constant loss (i.e., iron loss) occurs during the whole day but copper loss occurs only when the transformer is loaded and would depend upon the magnitude of load.

Consequently, the copper loss varies considerably during the day and the commercial efficiency of such transformers will vary from a low value (or even zero) to a high value when the load is high.

The performance of such transformers is judged on the basis of energy consumption during the whole day (i.e., 24 hours). This is known as all day efficiency or energy efficiency.

What is All day Efficiency?

The ratio of output in kWh to the input in kWh of a transformer over a 24-hour period is known as all day efficiency.

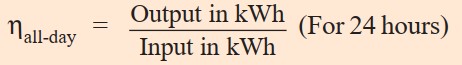
All day efficiency of transformer

All day efficiency is of special importance for those transformers whose primaries are never open-circuited but the secondary carry little or no load much of the time during the day.

In the design of such transformers, efforts should be made to reduce the iron losses which continuously occur during the whole day.

Note. The efficiency of a transformer means commercial efficiency unless stated otherwise.

Read : Percentage Impedance of Transformer

All day efficiency of transformer Solved Problems

Here are some problems and multiple-choice questions (MCQs) based on the all-day efficiency of a transformer, along with their solutions.

Problem 1

A 50 kVA, 2400/240 V transformer has a core loss Pc = 200 W at rated voltage and a copper loss Pcu = 500 W at full load. Determine the all-day efficiency of the transformer using the following load cycle.

% Load	0.0%	50%	75%	100%	110%
Power factor	–	1	0.8 lag	0.9 lag	1
Hours	6	6	6	3	3

Load Cycle of 50 kVA, 2400/240 V transformer

Problem 1 Solution

To determine the all-day efficiency of the transformer, we need to calculate the energy consumed by the transformer over the course of a day, both in terms of the energy it delivers to the load and the energy it consumes itself.

η_all-day = Energy output in kWh for 24 hrs / Energy input in kWh for 24 hours

Energy output over 24 hours

= 0 + (0.5 × 50 × 6) + (0.75 × 50 × 0.8 × 6 )+ (1 × 50 × 0.9 × 3) + (1.1 × 50 × 1 × 3) kWh
= 630 kWh

Energy losses over 24 hours:

Core loss

Copper loss

= 0.2 × 24 = 4.8 kWh

= 0.5² × 0.5 × 6 + 0.75² × 0.5 × 6 + 1² × 0.5 × 3 + 1.1² × 0.5 × 3
= 5.76 kWh

Total energy loss

= 4.8 + 5.76 = 10.56 kWh

All day Efficiency

η_all-day

= [630 / (630 + 10.56)] × 100% = 98.35%

Therefore all day efficiency of the transformer for the given load cycle is 98.35%.

Problem 2

Find the all-day efficiency of a 500 kVA distribution transformer whose copper and iron losses at full load are 4.5 kW and 3 kW respectively. During a day of 24 hours, it is loaded as under:

No. of hours	6	6	8	4
Load in kW	450	300	150	0
Power factor	0.9	0.75	1	–

Load Cycle of 500 kVA distribution transformer

Problem 2 Solution

To calculate the all-day efficiency of the transformer, we need to first calculate the energy losses in the transformer over 24 hours.

Given, the full load losses of the transformer are:

Copper losses: 4.5 kW
Iron losses: 3 kW

The transformer is loaded as follows:

6 hours at 450kW and 0.9 power factor
6 hours at 300 kW and 0.75 power factor
8 hours at 150 kW and 1 power factor
4 hours at 0 kW

Copper loss at any other load will be proportional to the square of the percentage of load.

Load in kW	P.F	Hours	kVA (Load in kW / P.F)	% of load (x)	Copper loss in kW (x² × P_cu(fl))	Copper loss in kWh	Iron Loss in kWh (kW * Hrs)	Output in kWh (load in kW * Hrs)
450	0.9	6	450/0.9 = 500	500/500 = 1	(1)² × 4.5 = 4.5	4.5 × 6 = 27	3 × 6 = 18	450 × 6 = 2700
300	0.75	6	300/0.75 = 400	400/500 = 0.8	(0.8)² × 4.5 = 2.88	2.88 × 6 = 17.28	3 × 6 = 18	300 × 6 = 1800
150	1	8	150/1 = 150	150/500 = 0.3	(0.3)² × 4.5 = 0.405	0.405 × 6 = 3.24	3 × 8 = 24	150 × 8 = 1200
0	–	6	0	0	0	0	3 × 6 = 18	0
					Total	47.52	72	5700