The percentage impedance of a transformer is marked on most nameplates – but what is it and what does the Z% figure mean?
The impedance of a transformer is the total opposition offered to alternating current. This may be calculated for each winding.
However, a rather simple test provides a practical method of measuring the equivalent impedance of a transformer without separating the impedance of the windings.
When referring to the impedance of a transformer, it is the equivalent impedance that is meant.
Definition of Percentage Impedance
The percentage impedance of a transformer is the volt drop on full load due to the winding resistance and leakage reactance expressed as a percentage of the rated voltage.
It is also the percentage of the normal terminal voltage required to circulate full-load current under short circuit conditions.
In other words, the percentage impedance of a transformer is the percentage of the rated voltage applied at one side (primary winding) to circulate rated current on transformer keeping its other side (secondary winding) under short circuit conditions.
It is marked in percentage value on the nameplate of power transformers in every electrical substation.
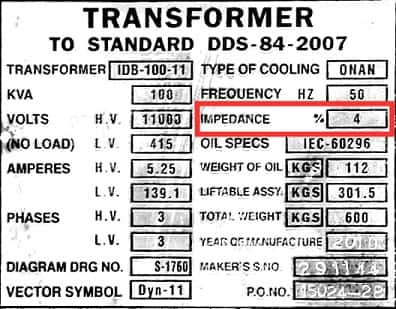
Explanation of Percentage Impedance
If we apply rated voltage at the primary winding of a transformer keeping its secondary winding short-circuited, then the amount of current at both windings will be extremely high as compared to the rated current.
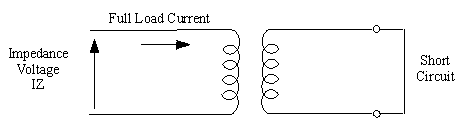
This current is called short circuit current and its magnitude is very high due to zero impedance offered by the load (secondary winding is short-circuited).
Now, if we reduce the applied voltage on the transformer primary i.e. we apply a percentage of rated voltage in transformer primary, current on both windings will also reduce.
At a particular percentage of rated voltage, the rated current will flow on transformer windings. This percentage of rated voltage at one side of the transformer which circulates rated current on transformer windings keeping its other side winding short-circuited is called percentage impedance of the transformer.
Calculation of Percentage Impedance
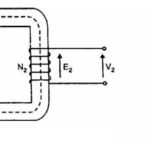
In order to determine equivalent impedance, one winding of the transformer is short-circuited. And a just enough voltage is applied to the other winding to create full load current to flow in the short-circuited winding.
This voltage is known as the impedance voltage.
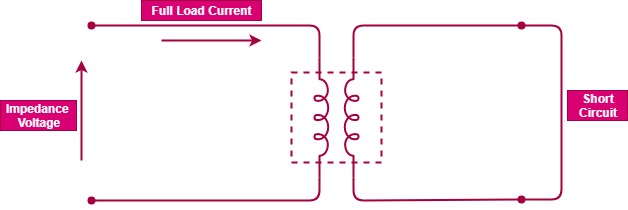
Either winding may be short-circuited for this test, but it is usually more convenient to short circuit the low-voltage winding.
The nameplate of a transformer shows its impedance value in percent. This means that the voltage drop due to the impedance is expressed as a percent of rated voltage.
Read More Here: How to Test Percentage Impedance of Transformer?
Example Calculation
For example, if a 2400/240 volt transformer has a measured impedance voltage of 72 volts on the high voltage windings, its impedance (Z), expressed as a percent, is:
Z% = (Impedance Voltage / Rated Voltage) x 100
percent Z = (72/2400)*100 = 3 percent
This means there would be a 72-volt drop in the high-voltage winding at full load due to losses in the windings and core. Only 1 or 2% of the losses are due to the core; about 98% is due to the winding impedance.
If the transformer were not operating at full load, the voltage drop would be less. If an actual impedance value in ohms is needed for the high-voltage side (Ohms Law):
Z = V/I
where V is the voltage drop or, in this case, 72 volts; and I is the full load current in the primary winding.
If the full load current is 10 amps:
Z = 72V/10A = 7.2 Ohms
Of course, one must remember that impedance is a combination of both resistive and reactive components.
Changing the Percentage Impedance Value
The most economical arrangement of core and windings leads to a ‘natural’ value of impedance determined by the leakage flux.
The leakage flux is a function of winding ampere-turns and the area and length of the leakage flux path.
These can be varied at the design stage by changing the volts per turn and the geometric relationship of the transformer windings.
The Effect of Higher and Lower Percentage Impedances
The percentage impedance of a transformer has a major effect on system fault levels. It determines the maximum value of current that will flow under fault conditions.
It is easy to calculate the maximum current that a transformer can deliver under symmetrical fault conditions.
By way of example, consider a 2 MVA transformer with an impedance of 5%. The maximum fault level available on the secondary side is:
2 MVA x 100/5 = 40 MVA
and from this figure, the equivalent primary and secondary fault currents can be calculated.
Role of Percentage Impedance in Short Circuit Calculations
Percentage impedance of transformer plays an extremely vital role in network calculation i.e.
- Short circuit calculation
- Voltage drop calculation.
As we discussed in the above section, when we apply rated voltage at the primary winding of a transformer whose secondary winding is short-circuited, short circuit current will flow on transformer windings.
The value of the short circuit current is,
Isc = Irated × 100/Z%
The value of percentage impedance is the same for both windings as it is the percentage of rated voltage. However, the value of the rated current will be different for primary and secondary windings. Accordingly, value of short circuit current will also be different for primary and secondary windings.
A less percentage impedance has both positive and negative effects.
If Z% of the transformer is less, the short circuit current will be more which will produce more stress in insulation. This is a negative factor.
On the other hand, it will reduce the voltage drop in the transformer winding. This will facilitate better voltage regulation. This is a positive factor.
Therefore the percentage impedance of the transformer has to be precisely selected to maintain a proper balance between fault level and voltage regulation.
Also Read: Percentage Reactance in Power System
Role of Percentage Impedance in Parallel Operation of Transformers
Percentage impedance has an important role in the parallel operation of transformers.
If the ratio of KVA rating to percentage impedance of two transformers operating in parallel is equal, they will share equal load. However, if the ratio is different, they will share the unequal load. This may result in the overheating of one transformer.
If the percentage impedances of the two parallel-connected transformers are different then also the parallel operation is possible. This is the case of unequal impedances ratio but the same kVA. This is commonly used when there are budget constraints. In this current divides in inverse proportions to the impedances and larger current flows through the smaller impedance. The lower percent impedance transformer can be overloaded when subjected to heavy loading while the other higher percent impedance transformer will be lightly loaded.
Permitted Tolerance in Z% of Transformer
The percentage impedance of a transformer is specified at the time of ordering. But it must be noted that IEC 60076 permits +1- 10% tolerance in percentage impedance at the manufacturer’s end.
Example: If we order a transformer with 8% percentage impedance, its actual Z% after manufacturing may be any value between 7.2% (-10% of 8) to 8.8% (+10% of 8), unless it is specifically agreed with the manufacturer at the time of ordering.
Tolerance in percentage impedance must be considered for power system calculations and accordingly system fault level & voltage regulation must be finalized.
Reference: IEEE C57.112.10
Please rephrase the beginning sentence “the total opposition offered an alternating current. ” I believe it does not make grammatical sense.
Using above recommendation to short circuit the secondary side, the percentage impedance is calculated to be 3%. Will this number also applies to the primary side?
When carrying out this test, will we expect also full load current on the short circuited secondary side? How long should this test last in order to measure the full load current on the primary side?
Thank you.
Thankyou for your valuable comment
I hope that you won’t stop writing such interesting articles. I’m waiting for more of your content. It’s so good that i’m going follow you!
It’s actually not clear to me why Z% it’s expressed in percentage. If the nominal voltage of a transformer is given (and it is built for that voltage), doesn’t it make more sense to express Z in absolute terms therefore in ohms?
Why bother if voltage applied to primary will always be the same?
Thanks.
It is convenient for the people that made the whole system, generators, step up transformer, transmissions lines, step down transformers, etc, in every segment there is a different nominal voltage and to make analysis, there is a need to transfer every component with its turns relations, so for identification the Z% it is a better practice
Z% is an expression of Impedance as a percentage of rated primary voltage
the reason for preferring the voltage applied to primary is ( short circuit test)
1-primary current is always less compared to secondary if transformer is step down. Under short circuit condition secondary and primary draws its rated current .so it is not practical to supply secondary rated current from our supply source with primary short circuited condition if transformer is step down .but if transformer is step up we can do this test with primary short circuited and supply voltage can apply to primary side.i hope answer is clear
2-if transformer is step up voltage can apply to secondary
I am glad it is a simple test to see the practical method of measuring the equivalent impedance of a transformer. This helps me know how to get a good transformer. I need one for my project so thank you.
https://www.linkedin.com/pulse/why-impedance-percentage-zfor-transformer-atham-soofi-us4xf/?trackingId=8OGOfgUDTnCp%2BedUbf0Gew%3D%3D
I have explained in my above article with easy to understand simple , it will clear all of your doubts
Thanks dear…
its really well explained…
keep it up…