Kirchhoff’s laws (KCL & KVL): Problems with Solution

Kirchoffs law problem 1

Welcome to the series of problems and solutions on Kirchhoff’s laws, specifically Kirchhoff’s Current Law (KCL) and Kirchhoff’s Voltage Law (KVL). In this article, we will explore various problems and solutions utilizing these fundamental principles in KCL and KVL. Join us as we delve into the application of Kirchhoff’s laws, offering a comprehensive understanding of their significance in solving complex circuit problems.

Kirchhoff’s laws Problem 1

Find i1, i2, and i3 in figure below

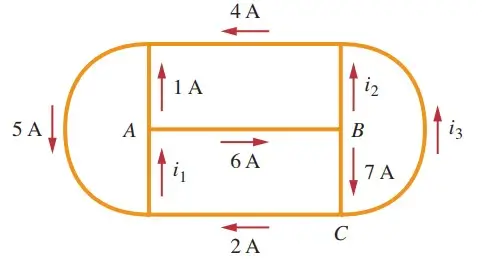
Kirchoffs law problem 1

Step by Step Solution:

To solve for $i_1​, i_2​$ and $i_3$​ using Kirchhoff’s laws, we can use Kirchhoff’s current law (KCL) which states that the total current entering a junction must equal the total current leaving the junction.

  1. Identify the junctions:
    • Junction A
    • Junction B
    • Junction C
  2. Apply Kirchhoff’s Current Law (KCL) at each junction:
    • At Junction A:
      • $i_1​=6A+1A= 7A$
    • At Junction B:
      • $6A=i_2+7A$
      • $i_2=-1A$
    • At Junction C:
      • $7A=i_3+2A$
      • $i_3=5A$

So, the currents are:

  • $i_1 = 7A$
  • $i_2 = -1A$
  • $i_3 = 5A$

These solutions satisfy Kirchhoff’s Current Law at all the junctions in the circuit.

Kirchhoff’s laws Problem 2

Determine $i_1$ and $i_2$ in the circuit below,

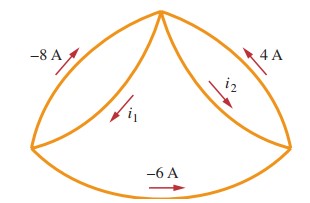
Kirchhoffs law problem 2

Step by Step Solution:

To solve for $i_1$​ and $i_2$​ using Kirchhoff’s laws, we can apply Kirchhoff’s current law (KCL) at the junctions in the circuit. Let’s denote the junction at the bottom left of the image as Junction 1, the top as Junction 2, and the bottom right as Junction 3.

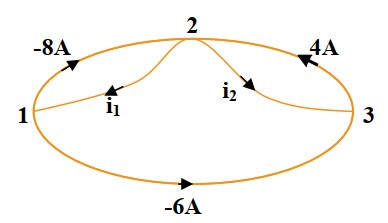
Kirchhoffs law problem 2 solution
  1. Identify the junctions and apply KCL:
    • At Junction 1: $-8+-6=\mathrm{i}_1\quad\longrightarrow\quad\mathrm{i}_1={-14\mathrm{A}}$
    • At Junction 3: $i_2+-6=\mathrm4\quad\longrightarrow\quad\mathrm{i}_2={10\mathrm{A}}$

Kirchhoff’s laws Problem 3

In the circuit below, calculate $V_1$ and $V_2$

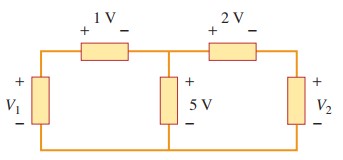
Kirchhoffs law problem 3

Step by Step Solution:

To solve for $V_1$​ and $V_2$​ using Kirchhoff’s laws, we will apply Kirchhoff’s Voltage Law (KVL), which states that the sum of all voltages around a closed loop is zero.

  1. Identify the loops in the circuit:
    • Left loop (containing $V_1$, the 1V voltage drop, and the 5V voltage drop)
    • Right loop (containing the 2V voltage drop, the 5V voltage drop, and $V_2$)
  2. Apply Kirchhoff’s Voltage Law (KVL) to each loop:
    • Left loop: Going clockwise: $V_1​−1V−5V=0 $
      • $V_1=6V$
    • Right loop: Going clockwise: $5V−2V-V_2=0$
      • $V_2 =3V$

Thus, the solutions for the voltages are:

  • $V_1​=6V$
  • $V_2 =3V$

These values satisfy Kirchhoff’s Voltage Law for both loops in the circuit.

Related Articles