Swinburne’s Test of DC Machine (Generator and Motor)

Swinburne’s Test
Swinburne’s test is the simplest indirect method of testing dc machines. In this method, the dc machine (generator or motor) is run as a motor at no-load and losses of the machine are determined. Once the losses of the machine are known, its efficiency at any desired load can be determined in advance.

It may be noted that this method is applicable to those machines in which flux is practically constant at all loads e.g., shunt and compound machines.

Read the testing of dc machines before reading this topic. 

Steps to find the Efficiency

Let us see how the efficiency of a dc shunt machine (generator or motor) is determined by this method. The test insists on two steps: 
  1. Determination of hot resistances of windings
  2. Determination of constant losses

Determination of hot resistances of windings

The armature resistance and shunt field resistance are measured at room temperature (say, at 15°C) using a voltmeter ammeter method (battery, voltmeter, and ammeter).

Since these resistances are measured when the machine is cold, they must be converted to values corresponding to the temperature at which the machine would work on full-load. 

Generally, these values are measured for a temperature rise of 40°C above the room temperature. From the data so obtained, different losses are computed and efficiency is determined.

Determination of constant losses

Please go through losses in dc machines for more details.

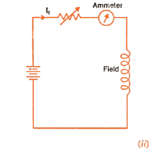
The machine is run as a motor on no-load with supply voltage adjusted to the rated voltage i.e. voltage stamped on the nameplate.

The speed of the motor is adjusted to the rated speed with the help of field regulator R as shown in figure (for more details please visit speed control of dc shunt motor).

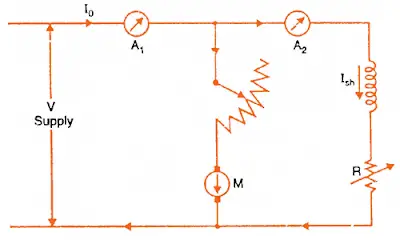
Swinburne’s Test
Swinburne’s Test for Determining Efficiency of DC Machine
Let V = Supply voltage
Io = No-load current read by ammeter A1
Ish = Shunt-field current read by ammeter A2.
∴ No-load armature current, Ia0 = Io – Ish
No-load input power to motor = V Io
No-load power input to armature = V Iao = V(Io – Ish)

Since the output of the motor is zero, the no-load input power to the armature supplies 

  1. iron losses in the core 
  2. friction loss
  3. windage loss
  4. armature Cu loss [ Iao2Ra or (Io – Ish)2Ra .
Constant losses, Wc = Input to motor – Armature Cu loss
Wc = V Io  – (Io – Ish)2Ra

Since constant losses are known, the efficiency of the machine at any other load can be determined. Suppose it is desired to determine the efficiency of the machine at load current I. Then,

Armature current, Ia = I – Ish … if the machine is motoring
    = I + Ish … if the machine is generating

Efficiency when running as a motor

Input power to motor = VI
Armature Cu loss = Ia2Ra  = (I – Ish)2Ra
Constant losses = Wc      found above
Total losses = (I – Ish)2Ra +Wc
∴ Motor efficiency, ηm = (Input – Losses)/Input = [VI – (I – Ish)2Ra +Wc]/VI

Efficiency when running as a generator

The output of generator= VI
Armature Cu loss = Ia2Ra  = (I + Ish)2Ra
Constant losses = Wc      found above
Total losses = (I + Ish)2Ra +Wc
∴ Motor efficiency, ηm = (Input – Losses)/Input = VI/[VI + (I + Ish)2Ra +Wc]

Advantages of Swinburne’s test

The following are the advantages of Swinburne’s test
  • The power required to carry out the test is small because it is a no-load test. Therefore, this method is quite economical.
  • The efficiency can be determined at any load because constant losses are known.
  • This test is very convenient.

Disadvantages of Swinburne’s test

The disadvantages of Swinburne’s test are given below
  • It does not take into account the stray load losses that occur when the machine is loaded.
  • This test does not enable us to check the performance of the machine on full-load. For example, it does not indicate whether commutation on full load is satisfactory and whether the temperature rise is within the specified limits.
  • This test does not give quite accurate efficiency of the machine. It is because iron losses under actual load are greater than those measured. This is mainly due to the armature reaction distorting the field.
author avatar

    2 Comments

  1. uwipgome
    May 17, 2019
    Reply

    I was searching for this for my exams in electrical machines. Thank you for sharing.

Leave A Reply

Your email address will not be published. Required fields are marked *

Copyright © 2020 Study Electrical, Inc.