In everyday language, the terms accuracy and precision are often used interchangeably. However, in the field of measurements, these terms have distinct meanings and implications. This article will explore the differences between accuracy and precision, their significance in measurements, and how they are applied in real-world scenarios.
What is Accuracy?
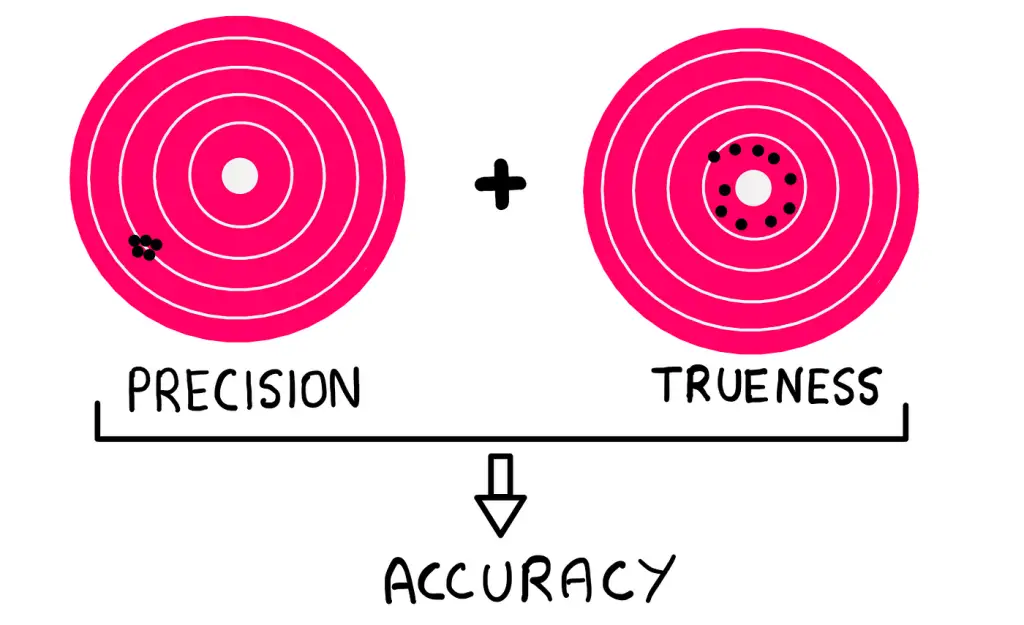
Accuracy refers to how close a measured value is to the true value of the quantity being measured. In other words, accuracy is about conformity to truth. It indicates the correctness of a measurement.
Ways to Express Accuracy
Accuracy can be expressed in several ways, depending on the context and the instrument being used:
- Point Accuracy
This refers to the accuracy of an instrument at a specific point on its scale. However, it does not provide information about the accuracy at other points on the scale. For a comprehensive understanding, a table specifying accuracy at multiple points across the instrument’s range is often used. - Accuracy as Percentage of Scale Range
For instruments with a uniform scale, accuracy can be expressed as a percentage of the scale range. For example, a thermometer with a range of 500°C and an accuracy of ±0.5% of the scale range would have an error of ±2.5°C at 500°C. However, at 250°C, the error would be ±1.25°C, which is 10% of the reading. This method can sometimes be misleading, especially at lower values. - Accuracy as Percentage of True Value
This is the most reliable way to express accuracy. It specifies the accuracy in terms of the true value of the quantity being measured. For example, an accuracy of ±0.5% of the true value means that as the readings decrease, so do the errors. This method ensures consistent accuracy across the entire range of measurements.
What is Precision?
Precision refers to the reproducibility of measurements. It measures how closely repeated measurements agree with each other, regardless of their accuracy. A precise instrument will produce consistent results, even if those results are not close to the true value.
Key Characteristics of Precision
Precision is composed of two main characteristics:
- Conformity: The degree to which repeated measurements agree with each other.
- Number of Significant Figures: The level of detail in the measurement, which indicates its precision.
Example of Precision vs. Accuracy
Consider an ammeter with a finely divided scale and a knife-edge pointer. It can measure current to 1/100 of an ampere, demonstrating high precision. However, if the ammeter’s zero adjustment is faulty, all readings will be consistently inaccurate. This shows that precision does not guarantee accuracy.
Another example is measuring a known voltage of 100V. If five readings are 104V, 103V, 105V, 103V, and 105V, the instrument has a precision of ±1% (since the maximum deviation from the mean is 1V) but an accuracy of only ±5% (since the readings deviate from the true value by up to 5V).

Indications of Precision
Precision is often indicated by:
- Consistency of Results: High precision means repeated measurements are closely clustered.
- Significant Figures: More significant figures indicate greater precision.
However, high precision does not always mean high accuracy. Systematic errors can cause all measurements to be biased in the same direction, leading to precise but inaccurate results.
Example of Precision Error
Consider measuring a resistor with a true resistance of 1,385,692Ω using an ohmmeter. If the observer can only read 1.4MΩ due to scale limitations, the measurement is precise (consistent) but not accurate. This is a precision error caused by the lack of significant figures.
Difference Between Accuracy and Precision
| Aspect | Accuracy | Precision |
|---|---|---|
| Definition | Closeness to true value | Reproducibility of results |
| Dependency | Can be affected by errors | Independent of true value |
| Improvement | Through calibration | Requires better equipment |
| Example | Hitting the target center | Hitting consistently close |
Significant Figures in Measurements
Significant figures are a key indicator of measurement precision. They convey the magnitude and precision of a quantity. The more significant figures, the greater the precision.
Examples of Significant Figures
- 256V: This has three significant figures, indicating the value is closer to 256V than to 255V or 257V.
- 256.0V: This has four significant figures, indicating the value is closer to 256.0V than to 255.9V or 256.1V.
Handling Large Numbers
Large numbers with zeros before the decimal point (e.g., 490,000) can be misleading. To avoid confusion, scientific notation is used. For example:
- 490,000 can be written as 4.9 × 10⁵, indicating two significant figures.
- 3,000,000 can be written as 3 × 10⁶, indicating one significant figure.
Rules for Counting Significant Figures
- Non-zero digits: Always significant.
- Zeros between non-zero digits: Significant.
- Leading zeros: Not significant.
- Trailing zeros with a decimal point: Significant.
- Trailing zeros without a decimal point: May or may not be significant depending on context.
Practical Examples
Example 1: Significant Figures in Measurements
- 302 A: 3 significant figures.
- 302.10 V: 5 significant figures.
- 0.00030 Ω: 2 significant figures (written as 30Ω).
- 5.01 × 10⁴: 3 significant figures.
- 502,000: 6 significant figures (or 3 if expressed as 502 × 10³).
Examples of Significant Figures
| Number | Significant Figures | Explanation |
| 302 A | 3 | Non-zero digits |
| 302.10 V | 5 | Trailing zero after decimal |
| 0.00030 Ω | 2 | Leading zeros not significant |
| 5.01 × 10⁴ | 3 | All shown digits are significant |
Key Takeaways
- Accuracy measures how close a measurement is to the true value.
- Precision measures how consistent repeated measurements are.
- High precision does not guarantee accuracy, and vice versa.
- Significant figures indicate the precision of a measurement.
- Use scientific notation to express large numbers clearly and avoid ambiguity.
By understanding the differences between accuracy and precision, and how they are expressed, you can ensure more reliable and meaningful measurements in your work. Always aim for both accuracy and precision, but remember that achieving one does not automatically guarantee the other.


